UAV design guidelines

These are design guidelines based on trends identified from the best data we can get for existing Unmanned Air Vehicles. These guidelines are for UAVs fitted with either four stroke or Wankel engines. Two stroke engines are not very fuel efficient, although they do have a high power-to-weight ratio. I have left off two stroke engines because we are mostly interested in long range UAVs that can be used in geophysical survey work. UAVs powered by gas turbines tend to be the larger UAVs, and these are at present not considered since we are in this case mostly interested in the smaller UAVs.

The design process for a UAV to be used in a survey application starts with the weight of the PayLoad Wpl and the Range. From the plot below we have deduced a relationship that allows one to estimate the take off weight, Wto. Remember these are guidelines for use with UAVs in which either four stroke or Wankel engines are used. The data used in the trend analysis has been based on:

TAM 5
Aerosonde I
Shadow 200
Hermes 180
Hermes 450
Predator MQ-1
Hermes 1500

1. Take off weight

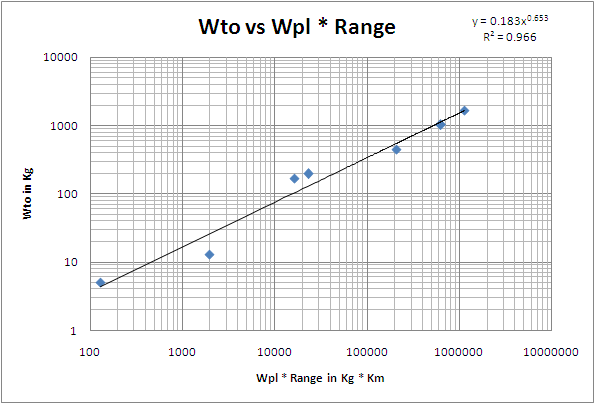
W_TakeOff = 0.183 * ( W_TakeOff * W_PayLoad )^0.653 = [Kg]

W_TakeOff = Wto = takeoff weight in Kg
W_Payload = Wpl = payload weight in Kg
Range in Km

2. Wingspan

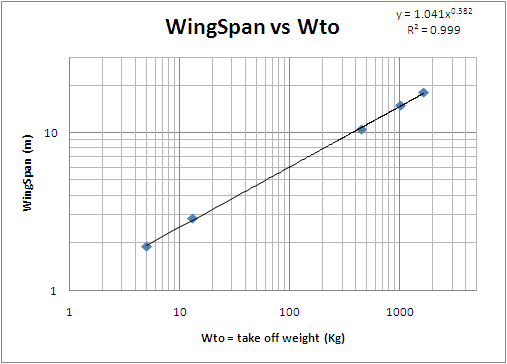
WingSpan = 1.041 * W_TakeOff^0.382 = [m]

W_takeoff = Wto = takeoff weight in Kgs
Data for the Shadow 200 and the Hermes 180 has not been included.

3. Length

Length = WingSpan / 1.775 = [m]

UAV	Wto [Kg]	wingspan = W [m]	length = L [m]	WS / L
Aerosonde I	13.1	2.86	1.74	1.644
Hermes 450	450	10.50	6.10	1.721
Predator MQ-1	1020	14.84	8.14	1.823
Hermes 1500	1650	18.00	9.40	1.915
			average	1.775

4. Endurance speed

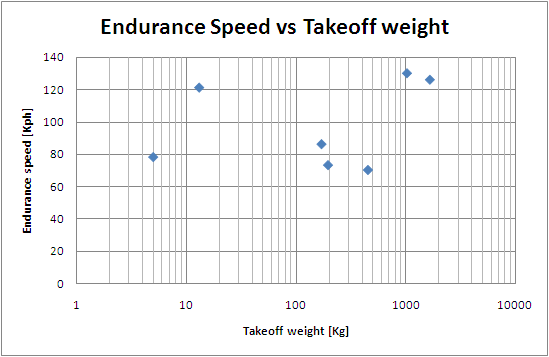
endurance speed vs take off weight for uav

Given the scatter in the above data, simply assume an endurance speed of 100 Kph.

endurance speed = V_endure = 100 Kph.

Typically, V_endure is from 75 to 125 Kph.

5. Endurance time

endurance time = T = Range / V_endure = [hr]

6. Weight of fuel

For a flight at constant speed, we have assumed the power required to keep the plane moving is directly proportional to the total weight of the plane, which decreases in a non-linear manner with time as the fuel is used up. The weight of the plane at a distance = x is given by W(x) = W to * exp( - x / D ), where W to is the take-off weight of the plane, and D is a figure-of-merit for the plane we call the "characteristic distance"

D = R / ln (W_to / W_nf )

where R is the range, W_to is the take off weight and W_nf is the weight of the plane with no fuel on board. For simplicity, it is assumed that at the end of the UAV flying a distance = R, there is no fuel left on the UAV.

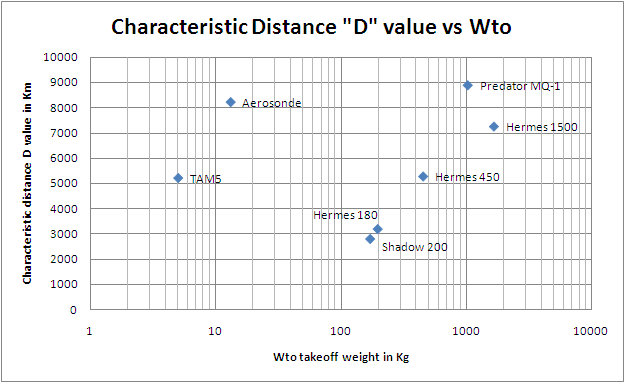
characteristic distance value vs take off weight for uav

Above is a plot of D figure-of-merit values for several well known UAVs. There is quite a spread. The higher the D value, the more efficient the UAV. The average value is 6,966 Km if we ignore the low values for the Shadow 200 and the Hermes 180. The Characteristic Distance "D" figure-of-merit value, or efficiency measure, for the UAV, is the distance the UAV flies per Kg of total, time dependent (since the UAV gets lighter as it uses up the fuel), aircraft weight.

weight of fuel = W_f = W_to * ( 1 - exp( - R / D ) = [Kg]

D = characteristic distance of the UAV = 7,200 Km from minimisation of sum of squares error values. Since the D value can vary so much from UAV to UAV, we have included this as an input parameter in the UAV Designer Utility.

W_f = weight of the plane with fuel on board, W_to = take-off weight

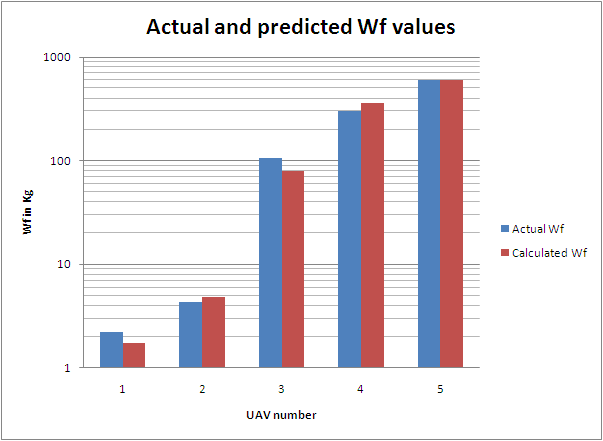
actual vs predicted weight of fuel values for uav

If we plot a histogram, as shown above, comparing the actual versus the predicted weight of the fuel for several UAVs, and then perform a least squares minimisation of the sum of the errors as a function of the D value, we conclude that we minimise the errors for the above UAVs when D = 7,200 Km. We have ignored the comparison for the Shadow 200 and the Hermes 180 since these two UAVs have low Characteristic Distance figures-of-merit.

7. Engine power

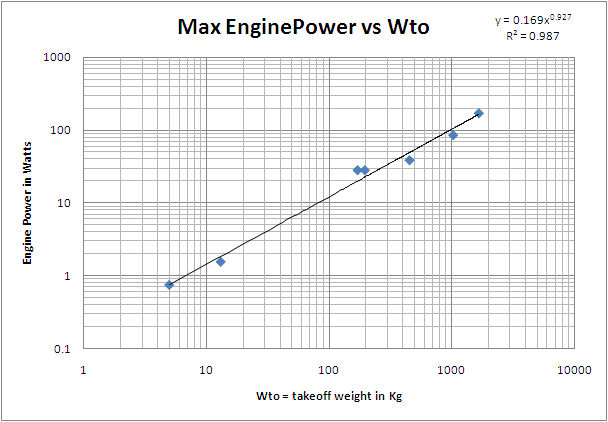
Maximum engine power = P_{eng_max} = 0.169 * W_to^0.927 = [Watts]

with W_to = the takeoff weight in Kg
we have included the electrical power required for the payload, and assumed an efficiency of 80% for the conversion of mechanical power into electrical power. Some brushless electrical motors have an efficiency rating above 80%.

8. Engine capacity

For a four stroke engine, Pout = 0.073 * x + 0.031 for Pout in KWatts, where x is the engine capacity in cc. The engine capacity = CAP is given by:

CAP = (P_{eng_max} - 0.031) / 0.073 = [cc]

The airframe weight includes the weight of the avionics.

9. Engine weight

For a 4 stroke engine, the power-to-weight ratio = R_ptw = 1.814 KW / Kg
For a Wankel engine, the power-to-weight ratio = R_ptw = 2.3 KW / Kg

Engine weight = W_eng = P_{eng_max} / R_ptw = [Kg]

W_eng = weight of the engine in Kg
P_{eng_max} = the maximum engine power in KWatts
R_ptw = the power-to-weight ratio for the engine in KWatts / Kg

10. Airframe weight

airframe + avionics weight = W_af = W_to - W_pl - W_f - W_eng = [Kg]

The airframe weight includes the weight of the avionics.

11. Price indication

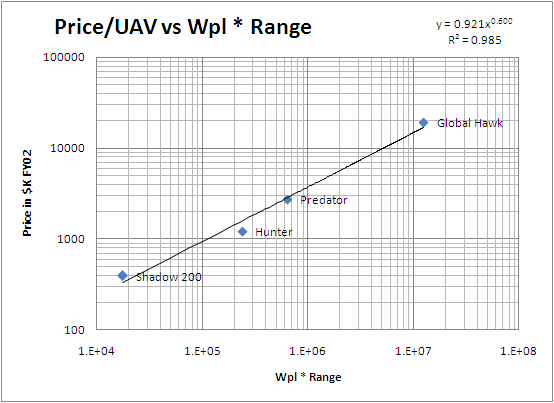
This is one of the most difficult charts, since we wish to remove the costs associated with the sensor systems that are typically to be found on military UAVs. Consequently, we have removed the data points for the Predator UAV and the Global Hawk UAV, since these UAVs carry very expensive avionics, communications and sensor systems.

estimated price per UAV = 0.921 * (W_pl * Range )^0.600 = [$K_FY02]

W_pl = weight of the payload in Kg
Range = range in Km

So, here you have the basis for a rudimentary Unmanned Air Vehicle design based on relationships derived from some existing UAVs. Additionally, you have a rough price guide, albeit based on FY02 $K values. Treat these estimates as very approximate guidelines.

The importance of the UAV life cycle

Above from the presentation by Peter Bockelmann on " The importance of logistics for all lifecycles of a UAV system" at the UAV 2007 Conference in Paris.